Topics

• Superstructure, as the ordering of some "property" on the initial crystal structure, may be realised as a result of phase transition under the action of temperature, magnetic field or pressure. Any crystal property localised on atom sites may be described by a Wannier-type function S defined on some set of equivalent positions in the unit cell. The respective function may be of scalar type - describing for example change of site occupation probability, polar vector type - describing for example displacements of atoms from their equilibrium positions, axial vector type - describing for example ordering of magnetic moments, or tensor type - describing for example ordering of quadrupolar moments. The description of this function in the usual reference frame, related to the crystallographic system axes, takes advantage of the translation symmetry only and the other symmetry relations of the crystal are lost in this description. As a consequence the description of many crystal properties is not as simple as could be.
  The refinement of unknown structure after the phase transition is very often required for X-ray or neutron diffraction experiment, and it takes place by comparison of calculated and measured diffraction patterns. For such procedure a model structure is required, defined by certain number of free parameters, and by variation of these parameters the „factor of disagreement” is minimised. The model structure, which gives the best fit to the experimental data, is chosen as the actual description of ordering in the phase under investigation. The procedure is convergent and resulting fit is more credible when the refinement starts from the good model structure, with as small number of free parameters as possible. This is the place, where the symmetry analysis method should be used. Phase transitions are usually followed by a change of symmetry, so all group-theoretical methods, which offer the possibility to understand all (not only the translational) symmetry relations between the old and new phases, are useful in this investigations. The presentation of model structures in the reference frame of basis vectors (BV) of irreducible representations (IR) of the initial symmetry group(instead of the frame of the crystallographic system) is the description best matching to the symmetry of the problem. It employs the symmetry of the wave vector found in the low symmetry phase and provides the simplest (including the lowest number of independent parameters) form of the structure description: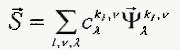
  
  where: (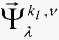- the basis vectors, l- number of k vector, n - number of IR, l=1....dim IR ) The form of BV-s is given by the theory and may be calculated for example by the computer program MODY. The coefficients C ^k,n_l of the linear combination of basis functions should be found from refinement procedure. The number of these unknown coefficients depends only on the number of IR taken into the model and their respective dimensions. As the BV-s are usually complex an additional restriction is imposed: the coefficients C ^k,n_l of the linear combination of basis functions should be selected in such a way that the resulting model has to provide only real values for atomic displacement from equilibrium positions or magnetic moments.This leads to a system of equations which gives the relations between the C^k,n _l. The above-mentioned system of equations can be reduced to a linearly independent set and then solved for the unknown coefficients. After such operation the final model contains clearly defined minimum number of free parameters and offers strictly defined relations between considered property on different crystal sites. These coefficients also form perfect order parameters for the phase transitions. The theory of representations allows their application in construction of invariants of the required symmetry group and further theoretical discussion.